Research

I have diverse interests in statistics and machine learning. Some recent topics that I enjoy thinking about are high-dimensional and nonparametric inference and some non-regular and/or high-dimensional parametric models. In addition to my theoretical interests, I am keenly interested in statistical applications in medical settings such as electronic medical records (EMRs) and personalized medicine. Below is a list of my papers and preprints discussing the aforementioned topics. For brief summaries click on the details button.

Preprints

Semi-supervised U-statistics with I. Kim, L. Wasserman and S. Balakrishnan [arXiv]DetailsThis paper proposes (among other results) optimal estimators of parameters defined through U-statistics in a semi-supervised setting.

Characterizing the minimax rate of nonparametric regression under bounded convex constraints with A. Prasadan [arXiv]DetailsThis paper derives the minimax rate in nonparametric regression where we relax an assumption imposed by classical works namely that the function class is bounded in sup norm.

Nearly Minimax Optimal Wasserstein Conditional Independence Testing with I. Kim, S. Balakrishnan and L. Wasserman [arXiv]Details This paper proposes a minimax optimal test (up to logarithmic factors) for testing conditional independence problem assuming Wasserstein-1 smoothness and Wasserstein-2 separation between the null and the alternative. The test statistic is novel and can be thought of as a weighted multi-resolution U-statistic.

Conditional Independence Testing for Discrete Distributions: Beyond \chi^2– and G-tests with I. Kim, S. Balakrishnan and L. Wasserman [arXiv]Details This paper proposes practical and effective conditional independence tests for discrete distributions.

Revisiting Le Cam’s Equation: Exact Minimax Rates over Convex Density Classes with S. Shrotriya [arXiv]DetailsThis paper proposes a small revision to Le Cam’s equation in nonparametric density estimation. The minimax rates for convex density classes are always determined by solving the equation \log M^{\mbox{\scriptsize loc}}_{\mathcal{F}}(\varepsilon, c) = n \varepsilon^2, where \log M^{\mbox{\scriptsize loc}}_{\mathcal{F}}(\varepsilon, c) is the local L_2 entropy of the density class \mathcal{F}.

A New Perspective on Debiasing Linear Regressions with Y. Yi [arXiv] DetailsIn this paper, we propose an abstract procedure for debiasing constrained or regularized potentially high-dimensional linear models. It is elementary to show that the proposed procedure can produce \frac{1}{\sqrt{n}}-confidence intervals for individual coordinates (or even bounded contrasts) in models with unknown covariance, provided that the covariance has bounded spectrum. While the proof of the statistical guarantees of our procedure is simple, its implementation requires more care due to the complexity of the optimization programs we need to solve. We spend the bulk of this paper giving examples in which the proposed algorithm can be implemented in practice. One fairly general class of instances which are amenable to applications of our procedure include convex constrained least squares. We are able to translate the procedure to an abstract algorithm over this class of models, and we give concrete examples where efficient polynomial time methods for debiasing exist. Those include the constrained version of LASSO, regression under monotone constraints, regression with positive monotone constraints and non-negative least squares. In addition, we show that our abstract procedure can be applied to efficiently debias SLOPE and square-root SLOPE, among other popular regularized procedures under certain assumptions. We provide thorough simulation results in support of our theoretical findings.

Non-Sparse PCA in High Dimensions via Cone Projected Power Iteration with Y. Yi [arXiv] DetailsIn this paper, we propose a cone projected power iteration algorithm to recover the first principal eigenvector from a noisy positive semidefinite matrix. When the true principal eigenvector is assumed to belong to a convex cone, the proposed algorithm is fast and has a tractable error. Specifically, the method achieves polynomial time complexity for certain convex cones equipped with fast projection such as the monotone cone. It attains a small error when the noisy matrix has a small cone-restricted operator norm. We supplement the above results with a minimax lower bound of the error under the spiked covariance model. Our numerical experiments on simulated and real data, show that our method achieves shorter run time and smaller error in comparison to the ordinary power iteration and some sparse principal component analysis algorithms if the principal eigenvector is in a convex cone.

Papers

Non-Asymptotic Bounds for the \ell_{\infty} Estimator in Linear Regression with Uniform Noise with Y. Yi [arXiv] [Bernoulli]DetailsThis paper shows some non-asymptotic bounds for the Chebyshev estimator, which is an unconventional alternative to least squares in regressions with uniform (or more generally bounded) noise. We also show that Chebyshev’s LASSO can be much more efficient than the regular LASSO under certain assumptions when the noise is uniform.

On the minimax rate of the Gaussian sequence model under bounded convex constraints [arXiv] [IEEE Trans. Inf. Theory]DetailsThis paper studies the minimax rate of the Gaussian sequence model under bounded convex constraints and shows that the rate can be equivalently expressed purely in terms of the local geometry of the constraint set K. The paper also contains an extension of the result for unbounded sets, under the assumption that the variance of the noise is known.

Local permutation tests for conditional independence with I. Kim, S. Balakrishnan and L. Wasserman [arXiv][AOS] DetailsWe explore “local” permutation tests for conditional independence. These tests shuffle the Y values if their corresponding Z values are close. Among other things we show that under some conditions such tests can be used to obtain minimax optimal testing procedures which do not require the specification of unknown constants.

Minimax Optimal Conditional Density Estimation under Total Variation Smoothness with M. Li and S. Balakrishnan [arXiv][EJS] DetailsThis paper studies the minimax rate of nonparametric conditional density estimation under a weighted absolute value loss function in a multivariate setting. We first demonstrate that conditional density estimation is impossible if one only requires that p_{X|Z} is smooth in x for all values of z. This motivates us to consider a sub-class of absolutely continuous distributions, restricting the conditional density p_{X|Z}(x|z) to not only be Holder smooth in x , but also be total variation smooth in z . We propose a corresponding kernel-based estimator and prove that it achieves the minimax rate. We give some simple examples of densities satisfying our assumptions which imply that our results are not vacuous. Finally, we propose an estimator which achieves the minimax optimal rate adaptively, i.e., without the need to know the smoothness parameter values in advance. Crucially, both of our estimators (the adaptive and non-adaptive ones) impose no assumptions on the marginal density p_Z , and are not obtained as a ratio between two kernel smoothing estimators which may sound like a go to approach in this problem.

Prior Adaptive Semi-supervised Learning with Application to EHR Phenotyping with M. Liu, Y. Zhang and T. Cai [arXiv][JMLR] DetailsElectronic Health Records (EHR) data, a rich source for biomedical research, have been successfully used to gain novel insight into a wide range of diseases. Despite its potential, EHR is currently underutilized for discovery research due to it’s major limitation in the lack of precise phenotype information. To overcome such difficulties, recent efforts have been devoted to developing supervised algorithms to accurately predict phenotypes based on relatively small training datasets with gold standard labels extracted via chart review. However, supervised methods typically require a sizable training set to yield generalizable algorithms especially when the number of candidate features, p , is large. In this paper, we propose a semi-supervised (SS) EHR phenotyping method that borrows information from both a small labeled data where both the label Y  and the feature set X are observed and a much larger unlabeled data with observations on Xonly as well as a surrogate variable S that is predictive of Y and available for all patients, under a high dimensional setting. Under a working prior assumption that S is related to X only through Y and allowing it to hold approximately, we propose a prior adaptive semi-supervised (PASS) estimator that adaptively incorporates the prior knowledge by shrinking the estimator towards a direction derived under the prior. We derive asymptotic theory for the proposed estimator and demonstrate its superiority over existing estimators via simulation studies. The proposed method is applied to an EHR phenotyping study of rheumatoid arthritis at Partner’s Healthcare.

Minimax Optimal Conditional Independence Testing with S. Balakrishnan and L. Wasserman [arXiv][AOS]Details We consider the problem of conditional independence testing of X and Y given Z where X,Y and Z are three real random variables and Z is continuous. We focus on two main cases — when X and Y are both discrete, and when X and Y are both continuous. In view of recent results on conditional independence testing (Shah and Peters 2018), one cannot hope to design non-trivial tests, which control the type I error for all absolutely continuous conditionally independent distributions, while still ensuring power against interesting alternatives. Consequently, we identify various, natural smoothness assumptions on the conditional distributions of X,Y|Z=z as z varies in the support of Z, and study the hardness of conditional independence testing under these smoothness assumptions. We derive matching lower and upper bounds on the critical radius of separation between the null and alternative hypotheses in the total variation metric. The tests we consider are easily implementable and rely on binning the support of the continuous variable Z. To complement these results, we provide a new proof of the hardness result of Shah and Peters and show that in the absence of smoothness assumptions conditional independence testing remains difficult even when X,Y are discrete variables of finite (and not scaling with the sample-size) support.

Tossing Coins Under Monotonicity [PMLR, AISTATS19]Details This paper considers the following problem: we are given n coin tosses of coins with monotone increasing probability of getting heads (success). We study the performance of the monotone constrained likelihood estimate, which is equivalent to the estimate produced by isotonic regression. We derive adaptive and non-adaptive bounds on the performance of the isotonic estimate, i.e., we demonstrate that for some probability vectors the isotonic estimate converges much faster than in general. As an application of this framework we propose a two step procedure for the binary monotone single index model, which consists of running LASSO and consequently running an isotonic regression. We provide thorough numerical studies in support of our claims.

Gaussian Regression with Convex Constraints [PMLR, AISTATS19]Details The focus of this paper is the linear model with Gaussian design under convex constraints. Specifically, we study the performance of the constrained least squares estimate. We derive two general results characterizing its performance – one requiring a tangent cone structure, and one which holds in a general setting. We use our general results to analyze three functional shape constrained problems where the signal is generated from an underlying Lipschitz, monotone or convex function. In each of the examples we show specific classes of functions which achieve fast adaptive estimation rates, and we also provide non-adaptive estimation rates which hold for any function. Our results demonstrate that the Lipschitz, monotone and convex constraints allow one to analyze regression problems even in high-dimensional settings where the dimension may scale as the square or fourth degree of the sample size respectively.

Isotonic regression meets LASSO [EJS]Details This paper studies a two step procedure for monotone increasing additive single index models with Gaussian designs. The proposed procedure is simple, easy to implement with existing software, and consists of consecutively applying LASSO and isotonic regression. Aside from formalizing this procedure, we provide theoretical guarantees regarding its performance: 1) we show that our procedure controls the in-sample squared error; 2) we demonstrate that one can use the procedure for predicting new observations, by showing that the absolute prediction error can be controlled with high-probability. Our bounds show a tradeoff of two rates: the minimax rate for estimating high dimensional quadratic loss, and the minimax nonparametric rate for estimating a monotone increasing function.

Misspecified nonconvex statistical optimization for sparse phase retrieval with Z. Yang, L. Yang, E. Fang, T. Zhao and Z. Wang [arXiv][Mathem. Program. Series B]DetailsExisting nonconvex statistical optimization theory and methods crucially rely on the correct specification of the underlying “true” statistical models. To address this issue, we take a first step towards taming model misspecification by studying the high-dimensional sparse phase retrieval problem with misspecified link functions. In particular, we propose a simple variant of the thresholded Wirtinger flow algorithm that, given a proper initialization, linearly converges to an estimator with optimal statistical accuracy for a broad family of unknown link functions. We further provide extensive numerical experiments to support our theoretical findings.

High-Temperature Structure Detection in Ferromagnets with Y. Cao and H. Liu [arXiv][Inf. Inference]Details This paper studies structure detection problems in high temperature ferromagnetic (positive interaction only) Ising models. The goal is to distinguish whether the underlying graph is empty, i.e., the model consists of independent Rademacher variables, versus the alternative that the underlying graph contains a subgraph of a certain structure. We give matching upper and lower minimax bounds under which testing this problem is possible/impossible respectively. Our results reveal that a key quantity called graph arboricity drives the testability of the problem. On the computational front, under a conjecture of the computational hardness of sparse principal component analysis, we prove that, unless the signal is strong enough, there are no polynomial time tests which are capable of testing this problem.

Property testing in high dimensional Ising models with H. Liu [arXiv] [AOS]Details This paper explores the information-theoretic limitations of graph property testing in zero-field Ising models. Instead of learning the entire graph structure, sometimes testing a basic graph property such as connectivity, cycle presence or maximum clique size is a more relevant and attainable objective. Understanding the statistical complexity of property testing requires the distinction of ferromagnetic (i.e., positive interactions only) and general Ising models. Using combinatorial constructs such as graph packing and strong monotonicity, we characterize how target properties affect the corresponding minimax upper and lower bounds within the realm of ferromagnets. On the other hand, by studying the detection of an antiferromagnetic (i.e., negative interactions only) Curie-Weiss model buried in Rademacher noise, we show that property testing is strictly more challenging over general Ising models. In terms of methodological development, we propose two types of correlation based tests: computationally efficient screening for ferromagnets, and score type tests for general models, including a fast cycle presence test.

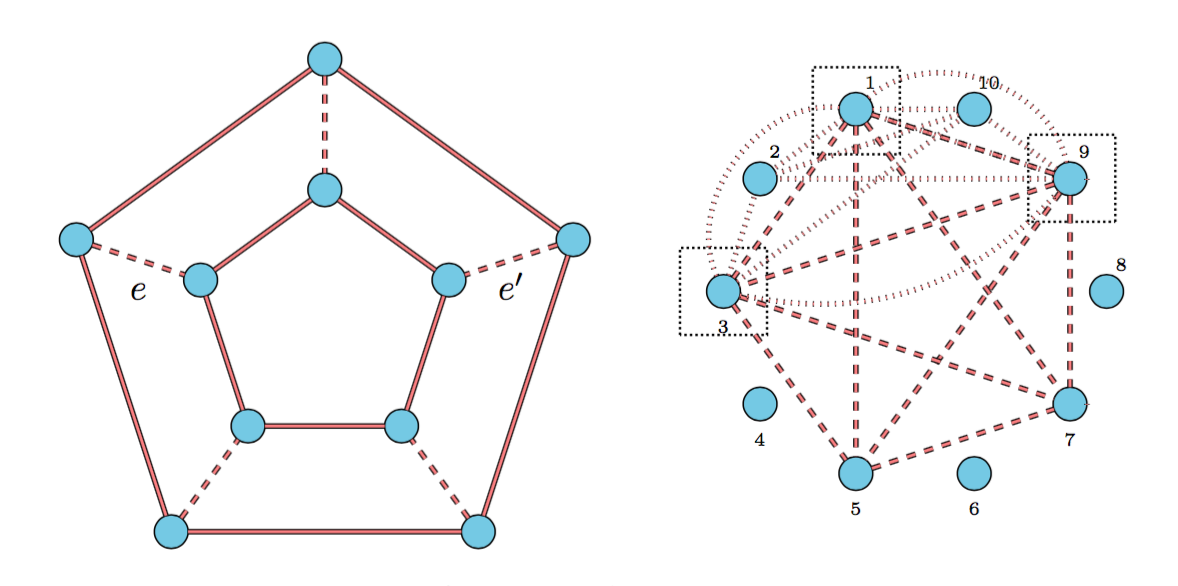
Combinatorial inference for graphical models with J. Lu and H. Liu [arXiv] [AOS] Details We propose a new family of combinatorial inference problems for graphical models. Unlike classical statistical inference where the main interest is point estimation or parameter testing, combinatorial inference aims at testing the global structure of the underlying graph. Examples include testing the graph connectivity, the presence of a cycle of certain size, or the maximum degree of the graph. To begin with, we develop a unified theory for the fundamental limits of a large family of combinatorial inference problems. We propose new concepts including structural packing and buffer entropies to characterize how the complexity of combinatorial graph structures impacts the corresponding minimax lower bounds. On the other hand, we propose a family of novel and practical structural testing algorithms to match the lower bounds. We provide thorough numerical results on both synthetic graphical models and brain networks to illustrate the usefulness of these proposed methods.

Connectivity and Clique

On the characterization of a class of Fisher-consistent loss functions and its application to boosting with J. S. Liu and T. Cai [pdf] [JMLR] Details Motivated by classification problems that arise in EMR settings, we propose a generic and robust boosting procedure which is able to work with non-convex loss functions. One key contribution is the relaxation of convexity required by Zou et al, as non-convex loss functions are less susceptible to outliers. We prove that in order to achieve Fisher consistency it suffices for a loss function \phi to satisfy
\phi(x) - \phi(x') \geq (g(x) - g(x'))k(x') for all x \in \mathbb{R}, x' \in \{z \in \mathbb{R} : k(z) \leq 0\},
where g,k are increasing and continuous functions satisfying further properties. The above condition relaxes convexity, which appears as a special case with g being the identity.

Support recovery for single index models in high-dimensions with Q. Lin and J. S. Liu [arXiv][AMSA] Details In this paper we study the support recovery problem for single index models Y=f(\boldsymbol{X}^{\intercal}\boldsymbol{\beta},\varepsilon), where f is an unknown link function, \boldsymbol{X}\sim N_p(0,\mathbb{I}_{p}) and \boldsymbol{\beta} is an s-sparse unit vector such that \beta_{i}\in \{\pm\frac{1}{\sqrt{s}},0\}. In particular, we look into the performance of two computationally inexpensive algorithms — the diagonal thresholding sliced inverse regression and a semi-definite programming (SDP) approach and show that support recovery can be successfully performed as long as the rescaled sample size \frac{n}{s \log p} is sufficiently large.

L_1–regularized least squares for support recovery of high dimensional single index models with Gaussian designs with J. S. Liu and T. Cai [arXiv][JMLR] Details We consider single index models of the type Y=f(\boldsymbol{X}^{\intercal}\boldsymbol{\beta},\varepsilon), where the predictor comes from a Gaussian design \boldsymbol{X} \sim N_p(0, \boldsymbol{\Sigma}). We show, somewhat surprisingly, that fitting an L_1-regularized least squares can recover the support of the single index model, in an optimal rescaled sample size, provided that the covariance satisfies the irrepresentable condition and the following key condition holds \mbox{Cov}(Y, \boldsymbol{X}^{\intercal}\boldsymbol{\beta}) \neq 0.

A unified theory of confidence regions and testing for high dimensional estimating equations with Y. Ning, J. S. Liu and H. Liu [arXiv] [Stat Sci]Details We propose a new inferential framework for constructing confidence regions and testing hypotheses in statistical models specified by a system of high dimensional estimating equations. We construct an influence function by projecting the fitted estimating equations to a sparse direction obtained by solving a large-scale linear program. Our main theoretical contribution is to establish a unified Z-estimation theory of confidence regions for high dimensional problems. As a result, our approach provides valid inference for a broad class of high dimensional constrained estimating equation problems, which are not covered by existing methods. Such examples include, noisy compressed sensing, instrumental variable regression, undirected graphical models, discriminant analysis and vector autoregressive models.

Agnostic estimation for misspecified phase retrieval models with Z. Wang and H. Liu [pdf], [NIPS 2016],[JMLR] Details This article considers a significant semi-parametric generalization of the sparse phase retrieval model Y = (\boldsymbol{X}^{\intercal} \boldsymbol{\beta})^2 + \varepsilon where \boldsymbol{X}\sim N_d(0,\mathbb{I}_{d}). The so-called misspecified phase retrieval (MPR) models take the form Y=f(\boldsymbol{X}^{\intercal}\boldsymbol{\beta},\varepsilon) and satisfy \mbox{Cov}(Y,( \boldsymbol{X}^{\intercal}\boldsymbol{\beta})^2) > 0. We propose an estimation procedure for agnostic estimation in misspecified phase retrieval, which consists of solving a cascade of two convex programs and provably recovers the direction of \boldsymbol{\beta}. Furthermore, we prove that our algorithm is minimax optimal over the class of MPR models. Interestingly, our minimax analysis characterizes the statistical price of misspecifying the link function in phase retrieval models. Below is a schematic illustration of the two-steps of our algorithm, showing how the second step estimate \hat{\boldsymbol{\beta}} improves on the first step estimate \hat{\mathbf{v}}.
AGENT: first step

Kernel machine testing for risk prediction with stratified case cohort studies with R. Payne, M. K. Jensen and T. Cai [Biometrics] Details In this article, we propose inverse probability weighted variance component type tests for identifying important marker sets through a Cox proportional hazards kernel machine regression framework under a case cohort sampling design (CCH). The CCH design introduces significant analytical complexity due to outcome-dependent, finite-population sampling. The proposed IPW test statistics have complex null distributions that cannot easily be approximated explicitly. The CCH sampling induces correlation which renders standard resampling methods such as the bootstrap useless for the purpose of approximating the distribution correctly. We, therefore, propose a novel perturbation resampling scheme that can effectively recover the induced correlation structure.

Kernel machine score test for pathway analysis in the presence of semi-competing risks with B. Hejblum and J. Sinnott [SMMR][CRAN] Details In cancer studies, patients often experience two different types of events: a non-terminal event such as recurrence or metastasis, and a terminal event such as cancer-specific death. Identifying pathways and networks of genes associated with one or both of these events is an important step in understanding disease development and targeting new biological processes for potential intervention. In this paper we propose a combined testing procedure for a pathway’s association with both the cause-specific hazard of recurrence and the marginal hazard of death. The dependency between the two outcomes is accounted for through perturbation resampling to approximate the test’s null distribution, without any further assumption on the nature of the dependency.

Classification of CT pulmonary angiography reports by presence, chronicity, and location of pulmonary embolism with natural language processing with S. Yu, K.K. Kumamaru, E. George, R.M. Dunne, A. Bedayat, A.R. Hunsaker, K.E. Dill, T. Cai, and F.J. Rybicki [JBI] Details In this paper we describe an efficient tool based on natural language processing for classifying the detail state of pulmonary embolism (PE) recorded in CT pulmonary angiography reports. The classification tasks include: PE present vs. absent, acute PE vs. others, central PE vs. others, and subsegmental PE vs. others. Statistical learning algorithms were trained with features extracted using the NLP tool and gold standard labels obtained via chart review from two radiologists. The areas under the receiver operating characteristic curves (AUC) for the four tasks using our approach show significant advantages over classifiers trained with standard text mining classifiers such as bag-of-words Naive Bayes type of classifiers.

Unpublished Manuscripts

Surrogate aided unsupervised recovery of sparse signals in single index models for binary outcomes with A. Chakrabortty, R. Carroll and T. Cai [arXiv] Details This work is motivated by modern studies involving large databases such as electronic medical records, where the outcome of interest Y is binary (i.e., a disease indicator) and unobserved. In addition to observing a predictor vector \boldsymbol{X} we assume that a surrogate variable S to the disease status Y is available. Importantly, the surrogate is only assumed to be accurately predictive of the disease status in the extremities of its support. Modeling the relationships between Y and S with the predictors via single index models, we obtain sharp finite sample guarantees on recovering the signal proportionally by simply fitting a least squares LASSO estimator to a subset of the observed data.

Adaptive Inferential Method for Monotone Graph Invariants with J. Lu and H. Liu [arXiv] Details We consider the problem of undirected graphical model inference. In many applications, instead of perfectly recovering the unknown graph structure, a more realistic goal is to infer some graph invariants (e.g., the maximum degree, the number of connected subgraphs, the number of isolated nodes). In this paper, we propose a new inferential framework for testing nested multiple hypotheses and constructing confidence intervals of the unknown graph invariants under undirected graphical models.

Software Packages

Our [CRAN] package performing the kernel machine test for pathway analysis in semi-competing risk settings.